Ответы на задания 3 тура по математике

1 задание Если числа натуральные, то это  1, 2, 3

 1 + 2 + 3 =1 * 2 * 3

Дополнение команды «Мыслители»:

«Получается, что результаты их сложения и произведения равны. Это свойство открыто пифагорейцами - последователями открытий Пифагора. Они считали, что числа правят миром, и в этом свойстве  шестёрки находили сакральный смысл. Число 6 считалось совершенным, так как ее половина - тройка, треть - двойка и, наконец, шестая часть - единица в сумме составляют целое число шесть.

Совершенными считались такие числа, сумма частей которых равнялась целому».

А если числа целые, то  -1, 1, 0; -2, 2, 0; -3, 3, 0; и т.д.

-1 + 1 + 0 = (-1) * 1* 0

2 задание В слове метрО, метр букв О,

(А в слове сорокА, сорок букв А).

3 задание Можно привести много вариантов.

Из ваших ответов:

33+33+33+3/3 =100…

33/0.33 = 100…

(111-11)*1=100

(222-22):2=100 …

99+9/9=100

111/1,11=100 …

7/7+7/7+7/7+(всего сто слагаемых)  = 100 …

111 – 11 = 100

33 · 3 + 3 : 3 = 100;

5 · 5 · 5 – 5 · 5 = 100

(5 + 5 + 5 + 5) · 5 = 100

100 = 5 · 5 · (5 – 5 : 5)

100 = (99 · 9 + 9) : 9

100= 1+1+1+1+…+1 (100раз по 1)

100 = 2+2+2+2+…+2 (50раз по 2)

100= 5+5+5+5+…+5 (20 раз по 5)

100=99+99:99 , 100= 99+999:999  …

Римскими цифрами:

100 = IIIIII…IIIII

100 = VVVVVVVVVVVVVVVVVVVV

100 = XXXXXXXXXX

100 = LL

100= С

 А может Дед Мороз любит программирование и знает, что в 99-ричной системе счисления 100 записывается как 11.

Ах, какая молодец команда «Арифметики», посмотрите на ее ответ.

4 задание  А) Из трех кружек крупы сварили кашу и поровну разделили ее на троих охотников.

Каждый съел кашу, приготовленную из одной кружки крупы. Первый охотник для приготовления каши дал два кружки крупы. Значит, кашу из одной кружки съел сам, а из второй угостил третьего охотника. Второй охотник накормил только себя. Получается, что все патроны достанутся первому охотнику.

Б) Команда «Аксиома»:

«Большая часть выдающихся людей, в том числе писателей, композиторов, актеров, художников, были заядлыми охотниками и считали это хобби лучшим времяпрепровождением и самыми вдохновляющими моментами в жизни. Описание охоты присутствует у признанных литературных классиков – Толстого, Тургенева, Хемингуэя. Тема охоты также часто увлекала великих художников. Одной из самых известных картин, посвященных охоте, является полотно Василия Перова «Охотники на привале», второе название – «Три охотника».

Василий Григорьевич Перов был страстным охотником. В последние годы жизни он даже стал корреспондентом журнала Сабанеева «Природа и охота», куда не только писал интересные зарисовки из своего опыта, но и разместил цикл теоретических статей об охоте. Конечно, любимое занятие не могло не быть запечатленным на полотнах художника. В 70-х гг. 18 века Перов создает серию картин, посвященных природе и отношению людей с ней – это такие полотна как «Голубятник», «Рыболов», «Птицелов», «Ботаник». А самой известной из этого цикла стала картина «Охотники на привале». Автором было написано два варианта картины: один хранится в Москве в Государственной Третьяковской Галерее (1871г.), а второй - в Санкт-Петербургском Русском Музее (1877г.)».

Команда «Бригантина»:

«Герои картины - реальные люди, друзья художника, послужившие прототипами охотников».

5 задание Цифра 3, глагол ТРИ (от глагола ТЕРЕТЬ) - повелительное наклонение единственного числа

6 задание Ответ команды  «Круг»:

 Эти равенства верны, если речь идет о часах:

1) 19 + 23 = 18 (через 23 ч после 19:00
     наступит 18:00 следующего вечера)

2)  21 + 8 = 5  (через 8 ч после 21:00
     наступит 5:00 следующего утра)

3)  12 + 12 = 0 (через 12 ч после 12:00
     наступит полночь, т.е. 0:00).

7 задание

8 задание  Три толстяка за три часа съедают три торта, получается, что один толстяк за три часа съедает один торт. Тогда за двенадцать часов один толстяк съест четыре торта. Следовательно, двенадцать толстяков за двенадцать часов съедят 48 тортов.

9 задание Посмотрите, как хорош ответ команды «Круг»

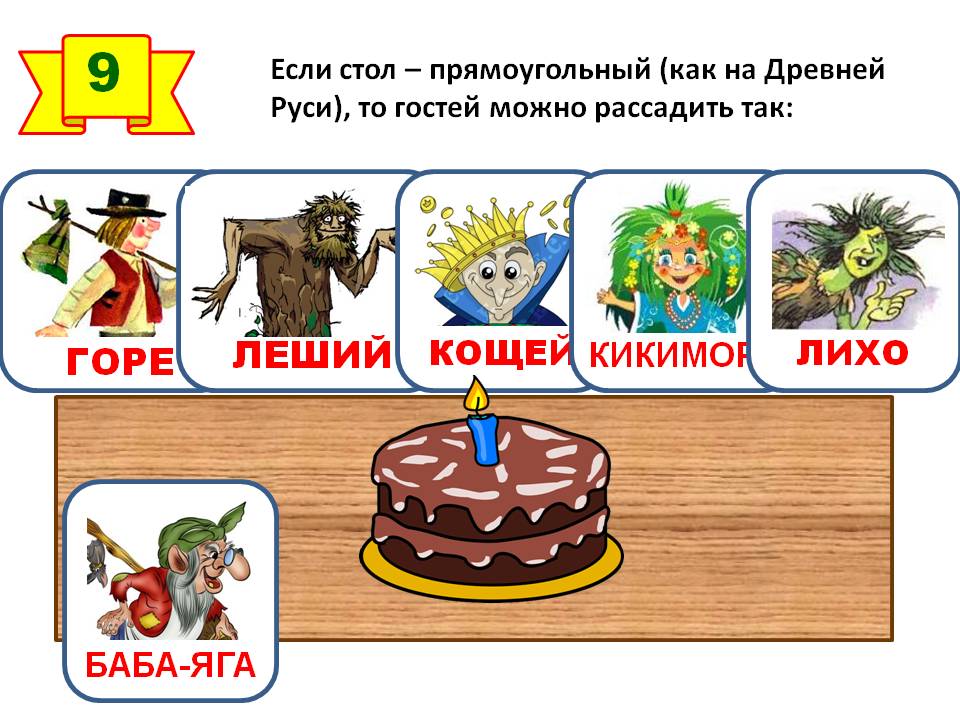
10 задание

1 способ. Дополнение до единицы.

Эти дроби правильные, меньше 1. Сократим дроби и посмотрим, какая из них находится на наибольшем расстоянии от 1.

 66/77=6/7 до единицы не хватает 1/7, 

555/666=5/6 до единицы не хватает 1/6,

4444/5555=4/5   до единицы не хватает 1/5, 

33333/44444=3/4 до единицы не хватает 1/4 - это  наибольшее расстояние от 1.

Значит, самая маленькая дробь 33333/44444.(аналогично можно проиллюстрировать на круге)

2 способ. Перевод в десятичную дробь.

7/8  = 0,875

66/77=6/7 = 0,857… (приблизительно равно)

555/666 =5/6 =0,8(3) (приблизительно равно  0.83333)

4444/5555 =4/5 = 0,8

33333/44444 = 0,75 – самая маленькая дробь.

3 способ. Сравнение остатков.

(без иллюстрации на круге, числовой прямой)

7/8

66/77=6/7

555/666=5/6

4444/5555=4/5

33333/44444=3/4

1-7/8=1/8

1-6/7=1/7

1-5/6=1/6

1-4/5=1/5

1-3/4=1/4

1/8<1/7<1/6<1/5<1/4

Чем меньше дробь, тем остаток больше.

Получаем, что самая маленькая дробь 33333/44444.

4 способ. Приведение к общему знаменателю.

Ответ команды «Интеграл».

Последние четыре дроби можно сократить: 66/77 = 6/7

555/666 = 5/6, 4444/5555 = 4/5, 33333/44444 = 3/4

Получили, что надо сравнить следующие дроби: 7/8, 6/7, 5/6, 4/5, 3/4

Для начала сравним 7/8 и 6/7, приведя к общему знаменателю 56, получим: 49/56 > 48/56. Значит 6/7 меньше7/8. Затем 5/6 и 4/5 приведем к общему знаменателю 30, получим:25/30 > 24/30. Значит 4/5 меньше 5/6. Возьмем две полученные меньшие дроби 6/7 и 4/5 и сравним их приведя к общему знаменателю 35, получим: 30/35 > 28/35. Значит  дробь 4/5 меньшая из первых четырех дробей. Осталось сравнить ее с последней дробью 3/4. Приведем дроби 4/5 и 3/4 к общему знаменателю 20 и сравним, получим:

16/20 > 15/20. Получили, что 3/4 самая маленькая дробь среди всех.

Получаем, что самая маленькая дробь 33333/44444.

1. Список используемых источников информации.
2. festival.1september.ru
3. ru.wikipedia.org
4. uchitmatematika.ucoz.ru
5. www.7gy.ru/detskoe-tvorchestvo
6. ped-kopilka.ru
7. www.myshared.ru
8. nazva.net/ru
9. rebus1.com
10. А.В.Спивак. Тысяча и одна задача по математике.: книга для учащихся 5-7 класса. – М.:Просвещение, 2005. – С.18.
11. И.Л.Бабинская, «Задачи математических олимпиад для 5-7 классов», 1971 г.
12. Ф.Ф. Нагибин, Е.С. Канин «Математическая шкатулка», М. Просвещение-1984.
13. Математические олимпиады "В СТРАНЕ СКАЗОК"    Астахов А.Ю.